Jupyter Notebook Integration with Quarto

Comprehensive guide to using Jupyter notebooks with Quarto for interactive data science and research
Published

February 11, 2024

Quarto seamlessly integrates with Jupyter notebooks, allowing you to write computational documents that combine code, output, narrative text, and visualizations. This page showcases the power of Jupyter notebooks within Quarto!

1 What are Jupyter Notebooks?

Jupyter notebooks are interactive computing environments that allow you to write and execute code in cells, mixing them with markdown documentation and visualizations. They’re particularly powerful for:

  • Data Analysis: Explore and visualize data interactively
  • Research: Document methodology and results together
  • Education: Create tutorials with executable examples
  • Reporting: Generate dynamic reports that update when data changes

2 Code Execution in Jupyter Notebooks

Let’s start with basic data analysis:

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns

# Set style for better-looking plots
sns.set_style("darkgrid")
plt.rcParams['figure.figsize'] = (12, 6)

# Create sample dataset
np.random.seed(42)
n = 100
data = pd.DataFrame({
    'x': np.linspace(0, 10, n),
    'y': np.linspace(0, 10, n) + np.random.normal(0, 1.5, n),
    'category': np.random.choice(['A', 'B', 'C'], n)
})

print("Dataset Summary:")
print(data.describe())
Dataset Summary:
                x           y
count  100.000000  100.000000
mean     5.000000    4.844230
std      2.930454    3.286129
min      0.000000   -1.556789
25%      2.500000    1.910049
50%      5.000000    4.588508
75%      7.500000    7.630459
max     10.000000   10.644887

3 Interactive Visualizations

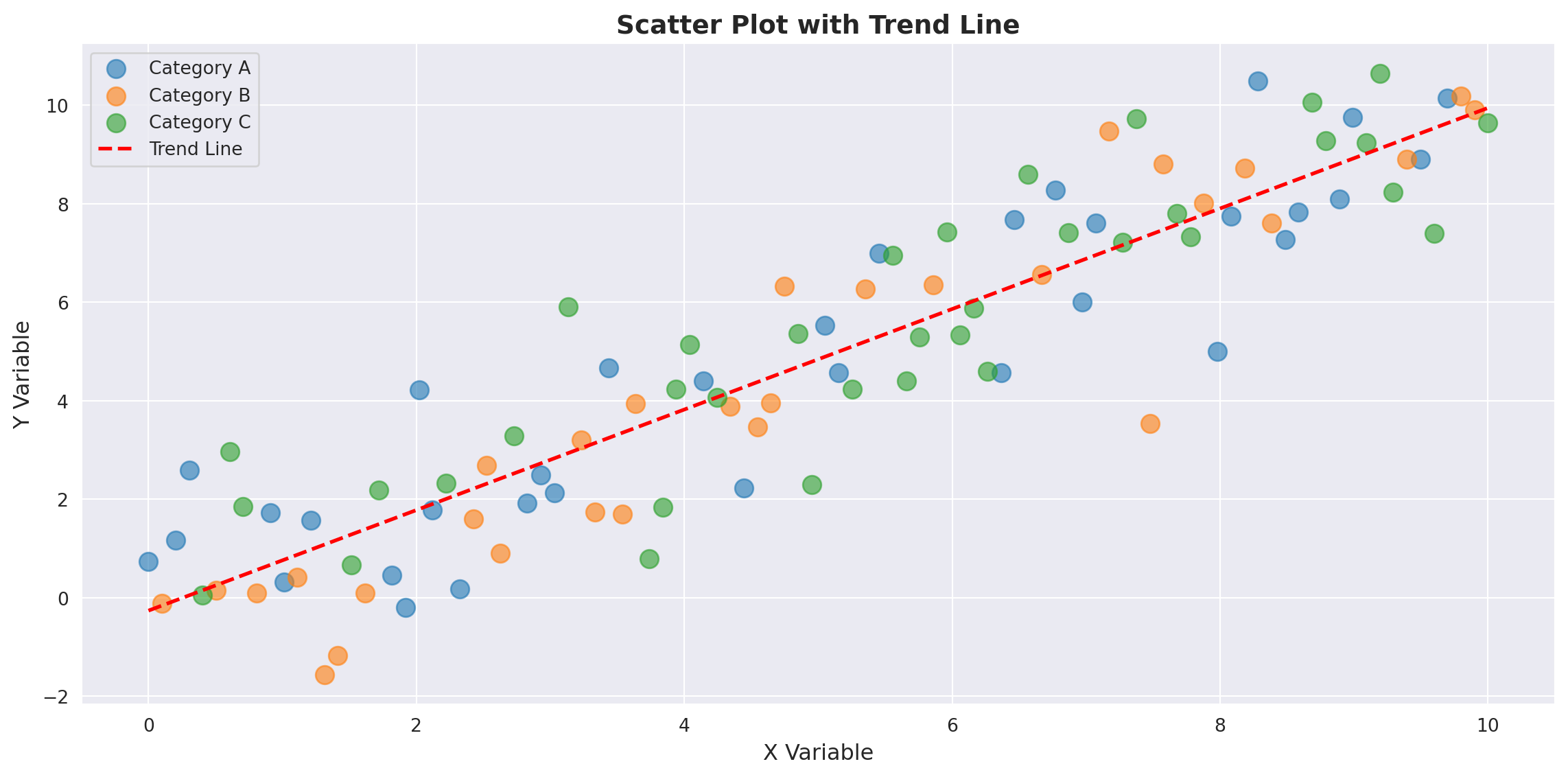
Create publication-quality plots directly in your documents:

# Create a scatter plot with regression line
fig, ax = plt.subplots()
for cat in ['A', 'B', 'C']:
    mask = data['category'] == cat
    ax.scatter(data[mask]['x'], data[mask]['y'], label=f'Category {cat}', alpha=0.6, s=100)

# Add trend line
z = np.polyfit(data['x'], data['y'], 1)
p = np.poly1d(z)
ax.plot(data['x'], p(data['x']), "r--", linewidth=2, label='Trend Line')

ax.set_xlabel('X Variable', fontsize=12)
ax.set_ylabel('Y Variable', fontsize=12)
ax.set_title('Scatter Plot with Trend Line', fontsize=14, fontweight='bold')
ax.legend()
plt.tight_layout()
plt.show()

print(f"\nTrend line equation: y = {z[0]:.3f}x + {z[1]:.3f}")


Trend line equation: y = 1.021x + -0.259

4 Statistical Analysis

Perform and document statistical tests:

from scipy import stats

# Test if groups are different
groups = [data[data['category'] == cat]['y'].values for cat in ['A', 'B', 'C']]
f_stat, p_value = stats.f_oneway(*groups)

print("ANOVA Test Results:")
print(f"F-statistic: {f_stat:.4f}")
print(f"P-value: {p_value:.4f}")

if p_value < 0.05:
    print("Result: Groups are significantly different (p < 0.05)")
else:
    print("Result: Groups are NOT significantly different (p >= 0.05)")
ANOVA Test Results:
F-statistic: 1.4797
P-value: 0.2328
Result: Groups are NOT significantly different (p >= 0.05)

5 Data Transformation and Processing

Show step-by-step data processing:

# Group by category and calculate statistics
grouped_stats = data.groupby('category').agg({
    'x': ['mean', 'std', 'min', 'max'],
    'y': ['mean', 'std', 'min', 'max']
}).round(3)

print("\nGrouped Statistics:")
print(grouped_stats)

# Create a new feature
data['z'] = data['x'] + data['y']
data['ratio'] = data['y'] / (data['x'] + 1)

print("\nFirst few rows with new features:")
print(data.head())

Grouped Statistics:
              x                            y                      
           mean    std    min     max   mean    std    min     max
category                                                          
A         4.777  3.108  0.000   9.697  4.674  3.250 -0.199  10.500
B         4.670  2.983  0.101   9.899  4.192  3.641 -1.557  10.190
C         5.485  2.726  0.404  10.000  5.549  2.949  0.053  10.645

First few rows with new features:
         x         y category         z     ratio
0  0.00000  0.745071        A  0.745071  0.745071
1  0.10101 -0.106386        B -0.005376 -0.096626
2  0.20202  1.173553        A  1.375573  0.976317
3  0.30303  2.587575        A  2.890605  1.985813
4  0.40404  0.052810        C  0.456851  0.037613

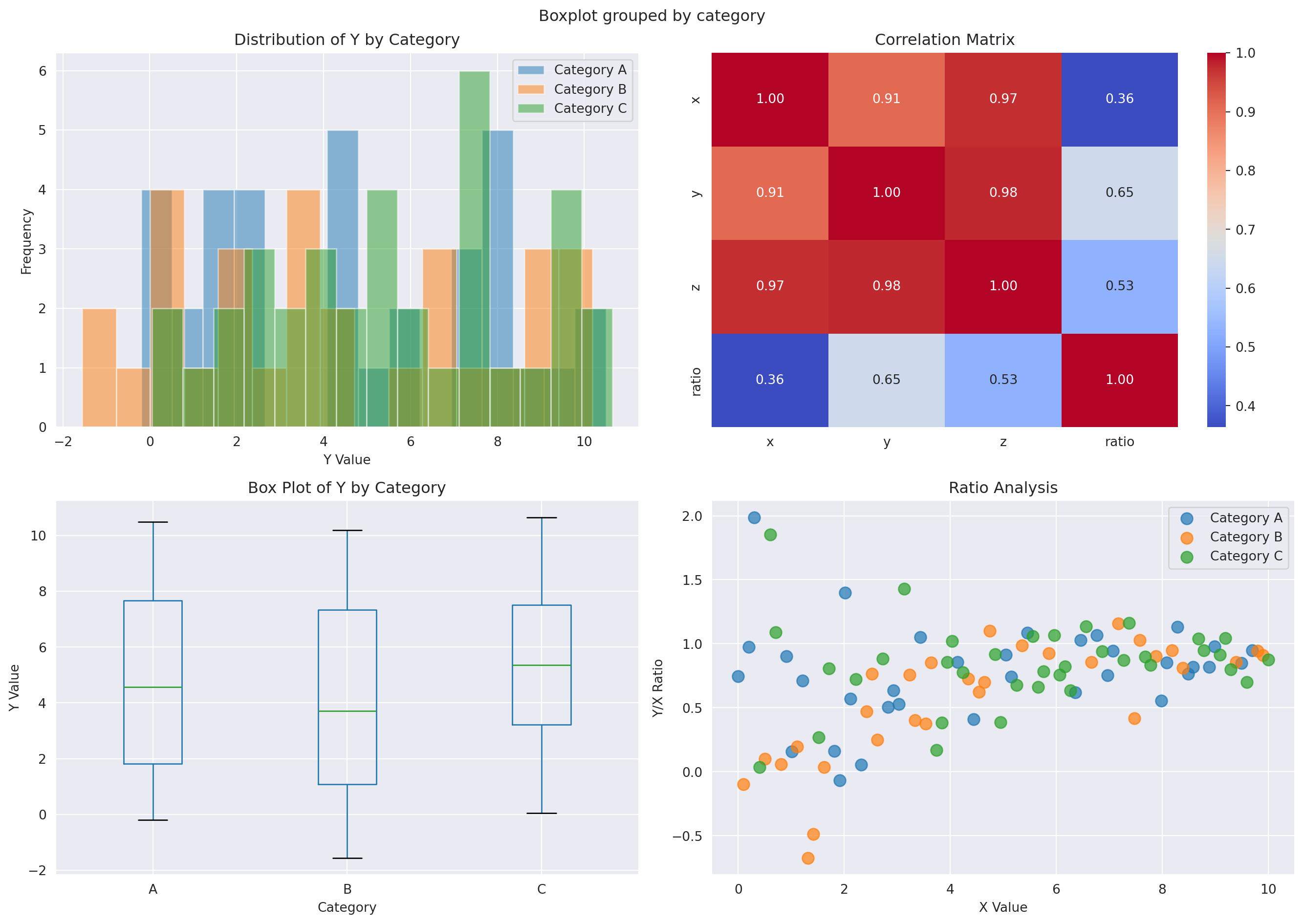
6 Advanced Visualization

Create more complex multi-panel visualizations:

fig, axes = plt.subplots(2, 2, figsize=(14, 10))

# Plot 1: Distribution of y by category
for cat in ['A', 'B', 'C']:
    mask = data['category'] == cat
    axes[0, 0].hist(data[mask]['y'], alpha=0.5, label=f'Category {cat}', bins=15)
axes[0, 0].set_xlabel('Y Value')
axes[0, 0].set_ylabel('Frequency')
axes[0, 0].set_title('Distribution of Y by Category')
axes[0, 0].legend()

# Plot 2: Heatmap of correlation
corr_data = data[['x', 'y', 'z', 'ratio']].corr()
sns.heatmap(corr_data, annot=True, fmt='.2f', cmap='coolwarm', ax=axes[0, 1], cbar=True)
axes[0, 1].set_title('Correlation Matrix')

# Plot 3: Box plot
data.boxplot(column='y', by='category', ax=axes[1, 0])
axes[1, 0].set_xlabel('Category')
axes[1, 0].set_ylabel('Y Value')
axes[1, 0].set_title('Box Plot of Y by Category')
plt.sca(axes[1, 0])
plt.xticks(rotation=0)

# Plot 4: Pair plot-like scatter
for i, cat in enumerate(['A', 'B', 'C']):
    mask = data['category'] == cat
    axes[1, 1].scatter(data[mask]['x'], data[mask]['ratio'], label=f'Category {cat}', s=80, alpha=0.7)
axes[1, 1].set_xlabel('X Value')
axes[1, 1].set_ylabel('Y/X Ratio')
axes[1, 1].set_title('Ratio Analysis')
axes[1, 1].legend()

plt.tight_layout()
plt.show()

TipBenefits of Jupyter Notebooks in Quarto
  • Reproducibility: Code and output are always in sync
  • Interactivity: Run code sections individually during development
  • Documentation: Mix code, results, and narrative seamlessly
  • Versioning: Track changes to computational documents in Git
  • Publishing: Export to HTML, PDF, or other formats
  • Collaboration: Share notebooks that others can run and modify

7 Machine Learning Example

A quick machine learning pipeline example:

from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error, r2_score

# Prepare data for modeling
X = data[['x', 'z']].values
y = data['y'].values

# Split data
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# Scale features
scaler = StandardScaler()
X_train_scaled = scaler.fit_transform(X_train)
X_test_scaled = scaler.transform(X_test)

# Train model
model = LinearRegression()
model.fit(X_train_scaled, y_train)

# Evaluate
y_pred_train = model.predict(X_train_scaled)
y_pred_test = model.predict(X_test_scaled)

train_r2 = r2_score(y_train, y_pred_train)
test_r2 = r2_score(y_test, y_pred_test)
test_mse = mean_squared_error(y_test, y_pred_test)

print("\nModel Performance:")
print(f"Training R²: {train_r2:.4f}")
print(f"Testing R²:  {test_r2:.4f}")
print(f"Test MSE:    {test_mse:.4f}")
print(f"\nModel Coefficients:")
for i, coef in enumerate(model.coef_):
    print(f"  Feature {i}: {coef:.4f}")
print(f"Intercept: {model.intercept_:.4f}")

Model Performance:
Training R²: 1.0000
Testing R²:  1.0000
Test MSE:    0.0000

Model Coefficients:
  Feature 0: -2.9160
  Feature 1: 6.0478
Intercept: 4.9489

8 Next Steps

Now that you understand the power of Jupyter notebooks in Quarto:

  1. Create your own: Write .ipynb files or .qmd files with code cells
  2. Explore interactivity: Add Observable JavaScript for client-side interactivity
  3. Build dashboards: Use Quarto dashboards to create interactive data apps
  4. Share knowledge: Publish your notebooks on GitHub or your personal website
ImportantLearn More

Happy data science! 🚀📊

PDF